CG -- Gram-Schmidt Conjugation

Motivation

To construct a set of A-orthogonal search directions $d_{(i)}$.

High-level idea

Use $n$ linearly independent vectors $u_0,u_1,...,u_{n-1}$. To construct $d_{(i)}$, take $u_i$ and subtract out any components that are not A-orthogonal to the previous $d$ vectors. In other words, set $d_{(0)}=u_0$, and for $i>0$, set

Find ${\beta }_{ik}$

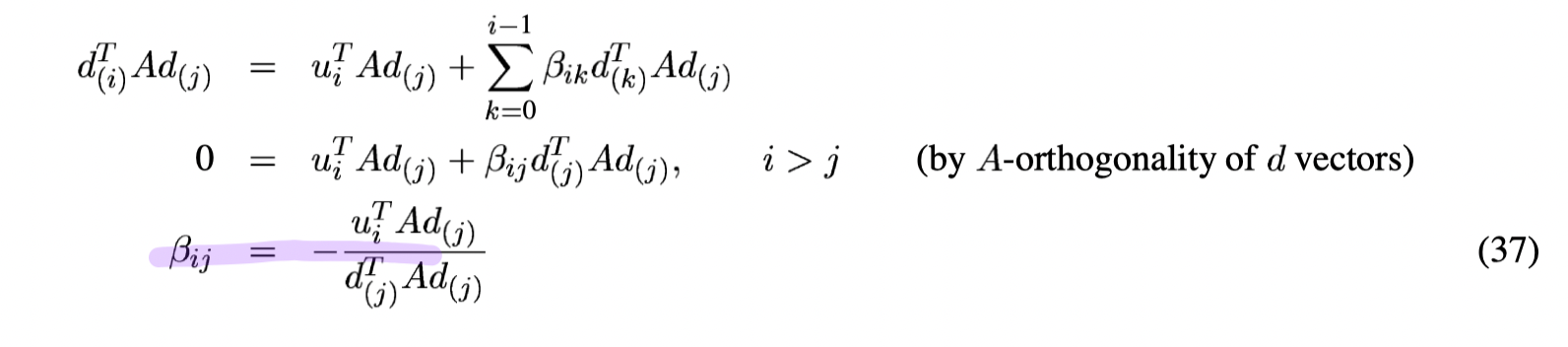
Difficulties

The difficulty with using Gram-Schmidt conjugation in the method of Conjugate Directions is that all the old search vectors must be kept in memory to construct each new one, and furthermore $O(n^3)$ operations are required to generate the full set.