CG -- The Method of Steepest Descent

Definitions

Whenever you read "residual", think "direction of steepest descent"

Procedure

1. Starting from an initial point $x_0$
2. compute $r_0=b-A{x}_0$, which is the direction
3. Select next point $x_1=x_0=\alpha r_0$

How to decide $r_0$

Choose the vector which has the minimized increase of $f$, where the projection on the direction line ($r_0$) is 0

Final procedure


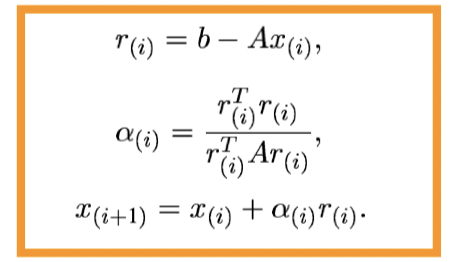
Convergency

CG -- Eigenvalues (Eigenvectors) and convergency

Several Special cases

We are using the Final procedure.

Special Case 1

If $e\mathrm{\_}(i)$ is an eigenvector with eigenvalue $\lambda \mathrm{\_}e$

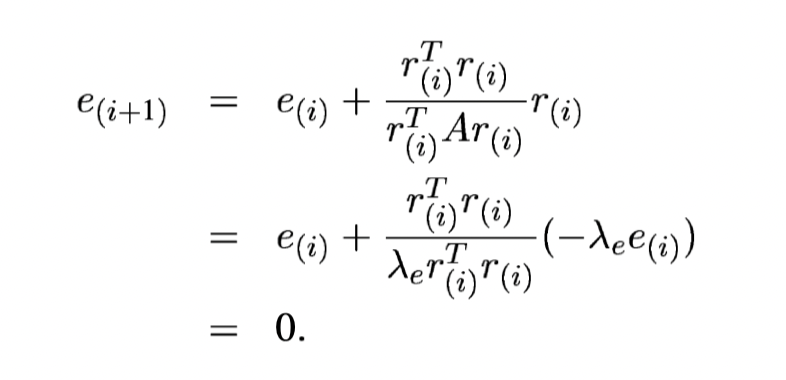
It takes only one step to converge to the exact solution

General Formula

If $e\mathrm{\_}(i)$ is a linear combination of eigenvectors, and if $A$ is symmetric, there exists a set of $n$ orthogonal eigenvectors of $A$. We have the following:

Then

Special case 2

If $e_{(i)}$ has only one eigenvector component, then convergency is also achieved in one step by choosing ${\alpha }_{(i)}={\lambda }_e^{-1}.$

Special case 3

All the eigenvectors have a common eigenvalue $\lambda$

General Convergency

We have the formula General Formula

Transfer minimizing $f(x)$ to a problem related to the energy norm

Recall for an arbitrary point $p$, and the solution point $x=A^{-1}b$, we have

(From Conjugate Gradient >
{ #6f2cce}
)

That is

Thus, minimizing $||e_{(i)}|{|}_A$ is equivalent to minimizing $f(x_{(i)})$


Express $\omega$ as condition number slop (we defined)


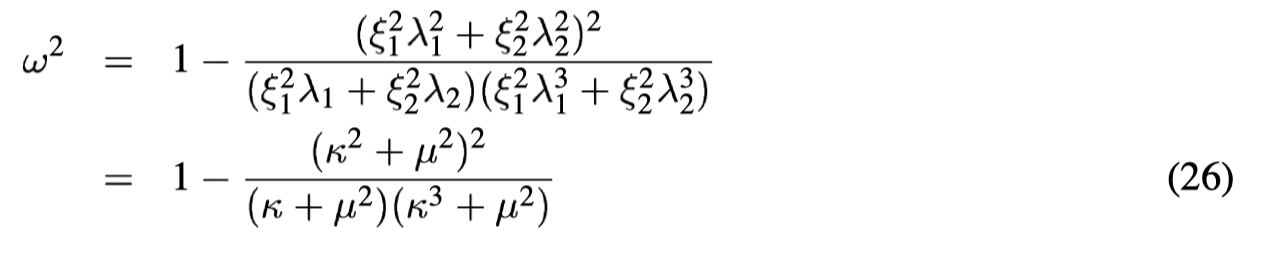
Plotting w.r.t. $\kappa$ and $\mu$


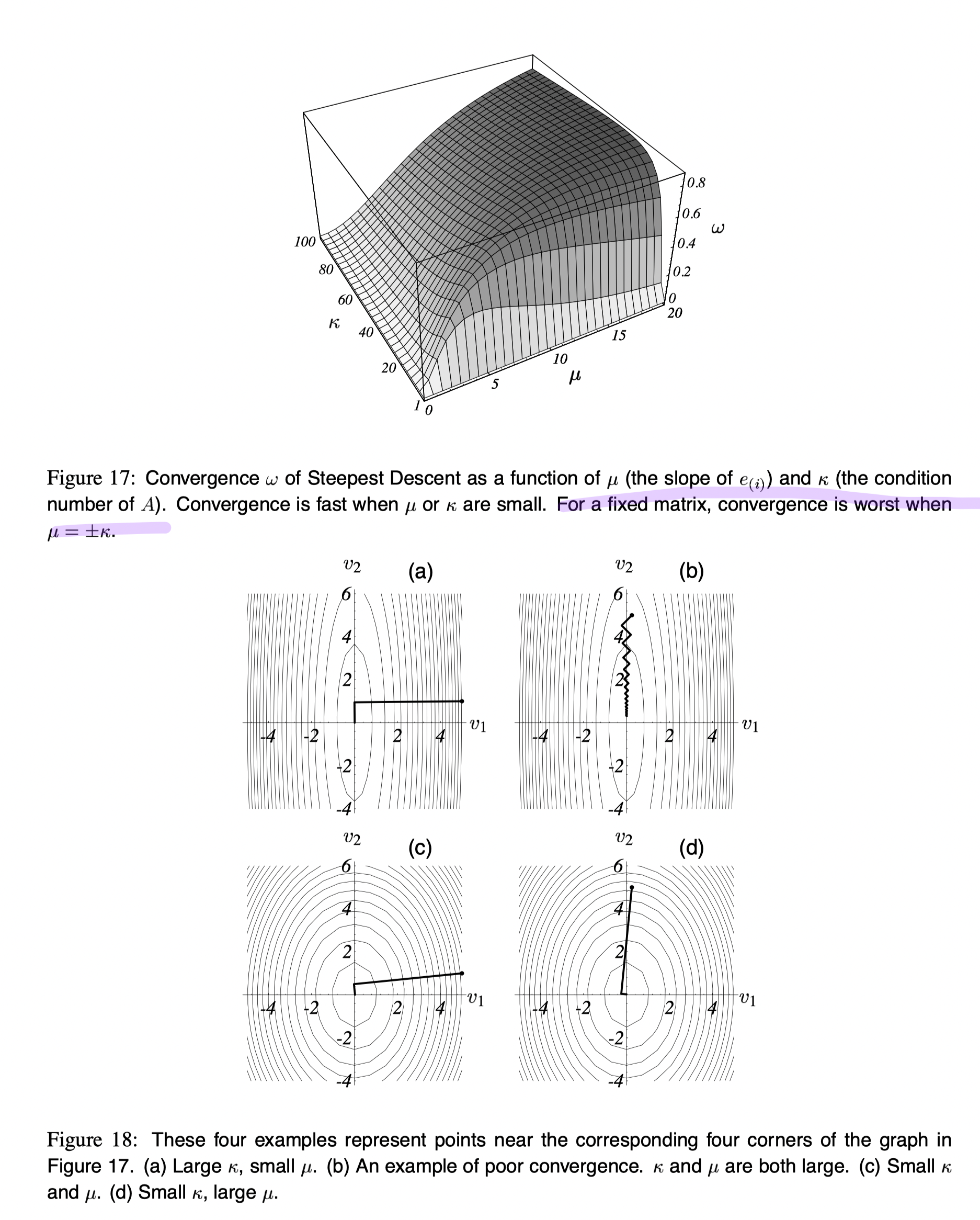
The worst case is when $\mu =\pm \kappa$
That is, the larger its condition number$\kappa$), the slower the convergence of in Steepest Descent.