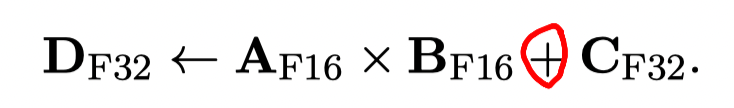Recovering single precision accuracy from Tensor Cores while surpassing the FP32 theoretical peak performance

Abstract

Motivation

Want to apply tensor cores to HPC algorithm
- such as preconditioners for iterative solvers and low-precision Fourier transforms

One solution

keep the mantissa loss in the conversion using additional half-precision variables and use them for correcting the accuracy of matrix-matrix multiplication

Limitation of this solution

still loss accuracy, not match the results of FP32 SIMT cores.

Take away of their method

1. Can match the FP32 SIMT cores without losing performance in the tensor cores.
2. The implementation is based on the CUTLASS
3. Key idea:
   • Deal with the rounding inside Tensor Cores
   • Deal with underflow probability during the correction computation
4. Specifications:
   • 51TFlop/s for a limited exponent range of FP16
   • 33TFlop/s for full exponent range of TF32
   • Tensor core has a theoretical peak performance of more than 300 TFlop/s; FP32 SIMT Core has a theoretical peak performance of 19.5TFlop/s.

Introduction

N.B.

1. Many architectures have the special units for low precision MMM.

   For instance, Google Tensor Processing Unit (TPU) [15], Intel Ponte Vecchio [13], IBM POWER10 [12], Preferred Networks MN-Core [24] and NVIDIA GPUs, all have special arithmetic units for low-precision matrix-matrix multiplication.

2. Already an approach to recover accuracy and is used in some libraries.

   Haidar [11] uses Tensor Cores within a mixed-precision iterative refinement solver in order to exploit the speed of Tensor Cores while recovering the accuracy through refinement. This method can be applied to recover full FP64 (IEEE binary64) accuracy and is currently used in MAGMA 1and NVIDIA’s cuSOLVER implementation().

3. Study on tensor cores

   Jia et al. and Raihan et al. analyze how Tensor Core assembly instructions divide the input matrices, and the order they compute multiplications of the subdivided matrices [14, 25].

   There have also been studies on how Tensor Cores support subnormal numbers and use RZ (Round toward Zero) [6].

   Others have performed error analysis of Tensor Cores, where the theoretical error bound of mixed-precision block FMA computation is analyzed and compared to the actual error of Tensor Cores [1].

   It has been also investigated that which part of computing precision is sensitive to the result [16]

Mukunoki et al.'s Error correction method

1. Mukunoki et al. uses the Ozaki scheme [23] on Tensor Cores [18] to refine the conversion of input matrices to FP16 result.
2. Good and bad
   • Recover single or double precision and can run FP64 faster in GeForce series.
   • Is very slow for FP32, and slow for FP64 in Tesla series.
   • Cannot fully recover the FP32 accuracy
3. High level idea
   > Using auxiliary FP16 variables to account for the truncated bits.

Feng's improved approach based on Mukunoki's

Uses a better rounding mode during the truncation to FP16

But they are still not able to match the accuracy of SGEMM with their error correction method.

Why these methods cannot match the accuracy

1. Didn't take into account the implicit bit.

   With the implicit bit the total bits of two FP16 numbers is actually (10 + 1) × 2 − 1 = 21 bits.

   • The implicit bit is the leading one in the normalized form.
2. $x_{hi}$ will always store the first (FP16's) 10 bits when truncating, but $x_{lo}$ does not always store the next (FP16's ) 10 bits.

The two main causes of error in existing work are:

1. Rounding mode (rtz by default)
2. High probability of underflow and gradual underflow in the error correction computation.

Evaluation baseline

• Markidis’ method
• Feng’s method
• cuBLAS SGEMM using FP32 SIMT Core
• cuBLAS SGEMM over Tensor Cores.

Key contribution

1. Evaluate Mantiss loss and find it is not the main cause.
2. Evaluate rounding loss and find it is one of the main causes.
3. Refine the rounding to make the accuracy match the FP32 SIMT.
4. Apply scaling to reduce underflow probability.
5. We remove one of the three error-correction terms, and reduce the amount of computation on Tensor Cores to 75% without loss of any accuracy.
   • What is the three error-correction terms.
6. Good results compared to baselines.

Background

Floating points - rounding

Markidis‘s correction to reduce mantissa loss when converting to FP16 matrix

1. Algorithm

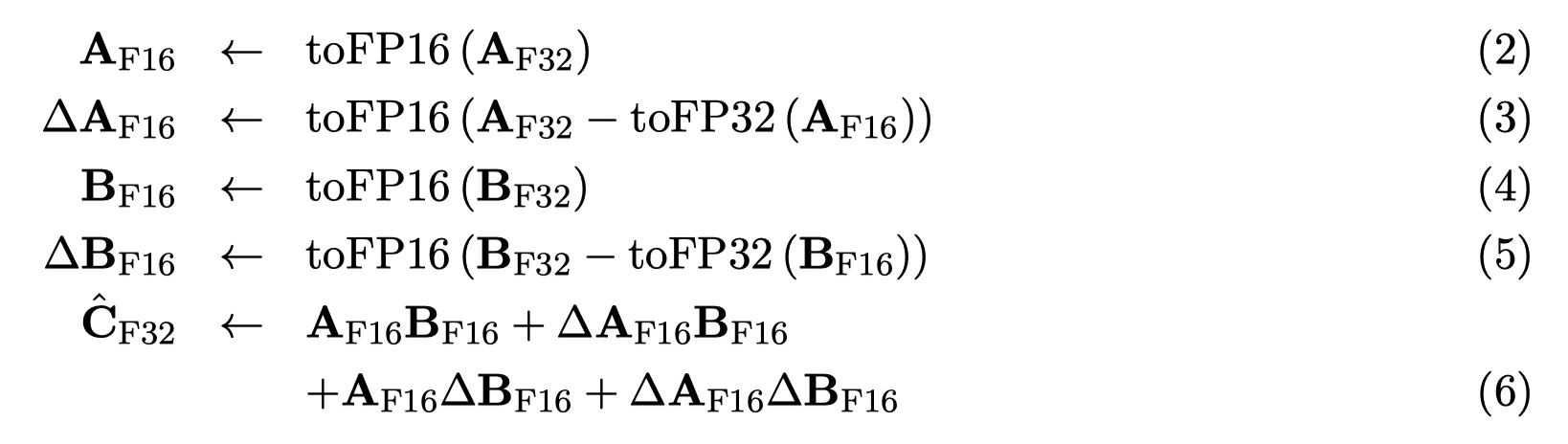
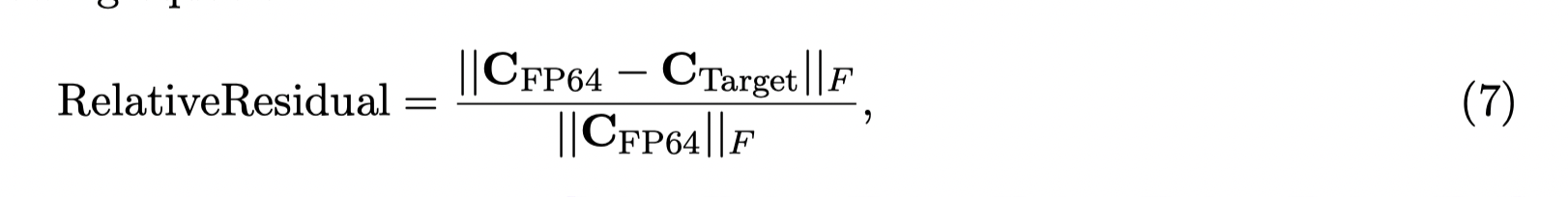
2. Accuracy Evaluation metric where $C_{FP64}$ is the reference matrix using FP64 to compute, i.e. $C_{FP64}=toFP64(A_{FP32})\cdot toFP64(B_{FP32})$

Error investigation and improvements

Evaluate the mantissa loss

1. Cause:
   For one element $v$, $v_{F16}+\mathrm{\Delta }{v}_{F16}$ cannot represent the full mantissa of $v_{F32}$
   • FP32 with 24 mantissa bits and FP16 with 11 mantissa bits, 24-11>11 -> two FP16 cannot hold the full 24 bits accuracy of FP32.
2. Compute the expectation of the mantissa length.
   • Full precision bits is 23
   • Expectation of the mantissa length for RN: 22.75
   • Expectation of the mantissa length for RZ: 22.5
   • RN is better than RZ since $\mathrm{\Delta }$ is negative (similar idea to complement can hold more bits.)
3. Experiments
   • Evaluate the accuracy (Relative Residual) by removing the last digit when computing.
   • Compare it to Markidis' method
     Result
4. Conclusion: Mantissa loss is not the main reason that their correction method is not accurate

Evaluate the rounding for TC accumulator and improved

1. Which rounding is evaluated
   • 
2. Conclusion: experiments show that applying RN to accumulator procedure is better than RZ when using Markidis‘s method
3. Question:
   • Any explanation?
   • Why adding 0? -> You have to add something in the Tensor Cores
4. Final workflow

Evaluate the probability of underflow when computing $\mathrm{\Delta }$

1. When computing
   $$\Delta v_{f16} = v_{fp32}- v_{fp16}$$
   it is easily to get underflow since these two values are very close.
2. The probability that underflow and graduate underflow occur will increase as the $|v_{32}|$ is approaching $2^{-15}$ (the limit of FP16)
   

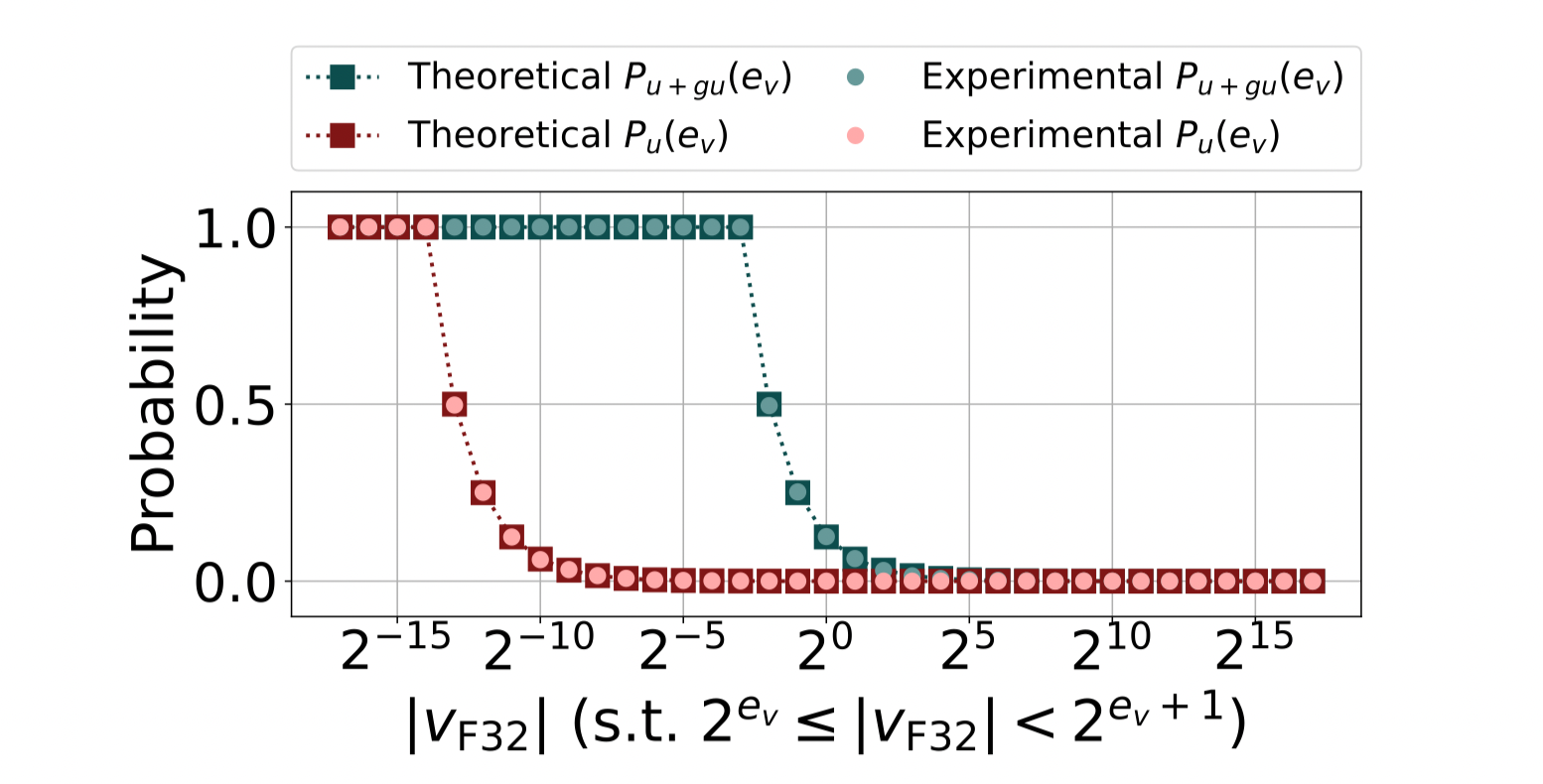
Method to reduce the probability of underflow

1. High-level idea: scaling when computing $\mathrm{\Delta }{v}_{f16}$

2. Algorithm
   

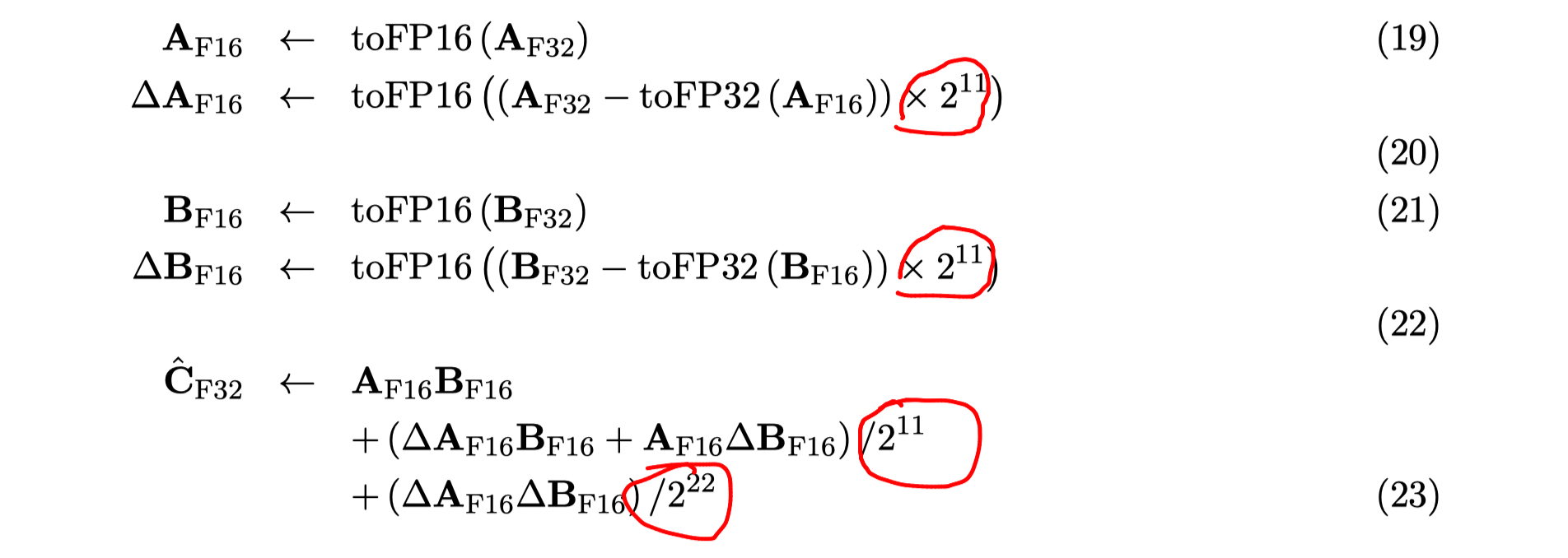
3. Alternatively, use TF32 since they have the same range as FP32.

Refine the algorithm

In equation (23), we have $A_{f16}Bf16+(\mathrm{\Delta }{A}_{f16}\mathrm{\Delta }Bf16)/2^{22}$. Notice that the second term can only affect the LSB of the first term so we can remove it.

Implementation

Just implement the algorithms in CUTLASS
Notice that they did a parameters search to optimize the throughput in CUTLASS.

Lessons

1. Statistical analysis of floating-point
   • Expectation of mantissa bits
   • Probability of underflow
2. Power consumption is one important aspect need to be considered when using half precision algorithm.

   In recent year, the real machines of quantum computer have been developed and tried to be shown quantum supremacy, that they compute certain tasks that (classical) supercomputers are not be able to compute in realistic time. Moreover, since they have low power consumption [2], energy efficiency is becoming an important metric when evaluating quantum supremacy. For instance, qFlex is a quantum computer simulator based on tensor network contraction using single-precision complex matrix-matrix multiplication, where the power consumption of each component was reported during its simulation on Summit V100 GPUs [28]. Although they have considered to use FP16 and Tensor Cores in their simulation, they decided not to use it since FP16 has less exponent than FP32 and insufficient to use.

Thoughts

• Use this method when mixed precision is not able to update?
• Current mixed precision didn't tackle underflow.
• Why just use TF32?
• Can FP64