Implement neural network

• Link: https://towardsdatascience.com/an-introduction-to-neural-networks-with-implementation-from-scratch-using-python-da4b6a45c05b

Philosophy

• Many variables determine the final result, but we don't know how many (what degree polynomials). Overfitting? Underfitting?
• Can we have a model that automatically generalizes and chooses the best fit for our data, which like the human brain, is not bound by the types of functions available
• Hidden layers represent some hidden variables that cannot be measurement or observed. The final output is decided by the the previous layer, but this layer summarize the knowledge from the previous layers.

The structure of neural network

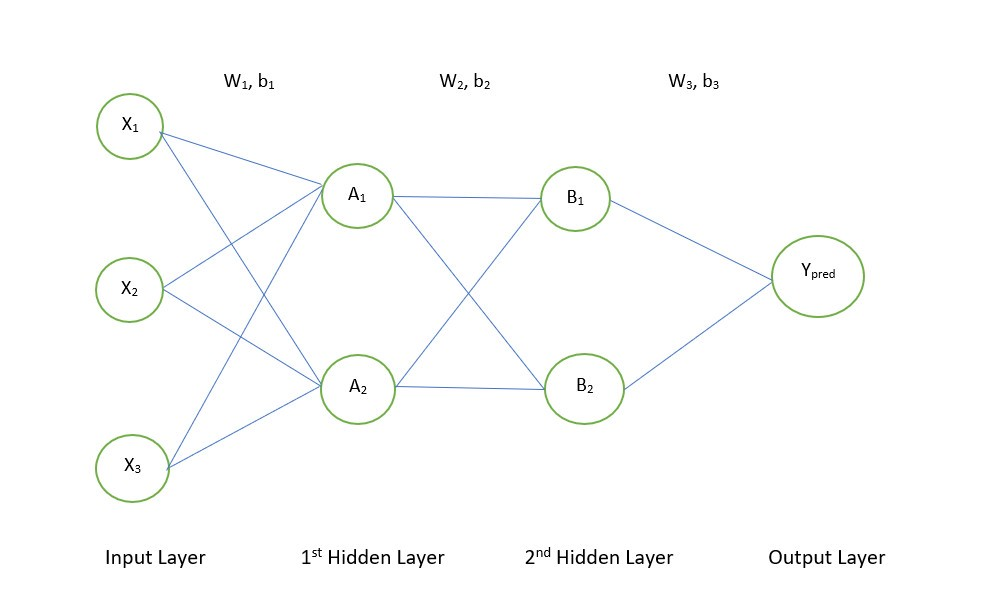
- This is a 3 layers neural network since the input layer is not counted

- E.g. A1 is the activation (or value ) of the first neuron in the first hidden layer.

- The weights are organized in the form of a matrix of shape (no of units in current layer, no of units in previous layer), The biases are organized in the shape of (no of units in current layer, 1).

E.g. W1.shape =(2,3), B1.shape=(2,1), $W_{0,1}$ is the wight from A1 to X2.

A1 = g(f(x1,x2,x3)) where f is a linear function using corresponding wight and bias, and g is an activation function,

Activation functions

$W_i$ and $B_i$ are the parameters we want to learn

Implementation

Goal

Minimize MSE (below) to lear $W_i$ and $B_i$

where $m$ is the number of data points.

Backpropagation - Find the gradients of the cost with respect to each of the wights and biases to tune

Optimizer to achieve the goal -- Gradient descent

Terminology

Layers of a network11

Activation functions

Why

Sigmoid

Disadvantage:

ReLU

Activation