Conjugate Gradient
Motivation
Solve large systems of linear equations
where
Why symmetric and Why positive
In short, if
This linear system problem can be transfer to an optimization problem
- We have a quadratic function of vector
- Gradient of
is - If
is symmetric Therefore, is critical point of . ( ) - If
is positive-define, that is for every nonzero vector , , is an increasing function and can be solved by finding an that minimizes .
Note
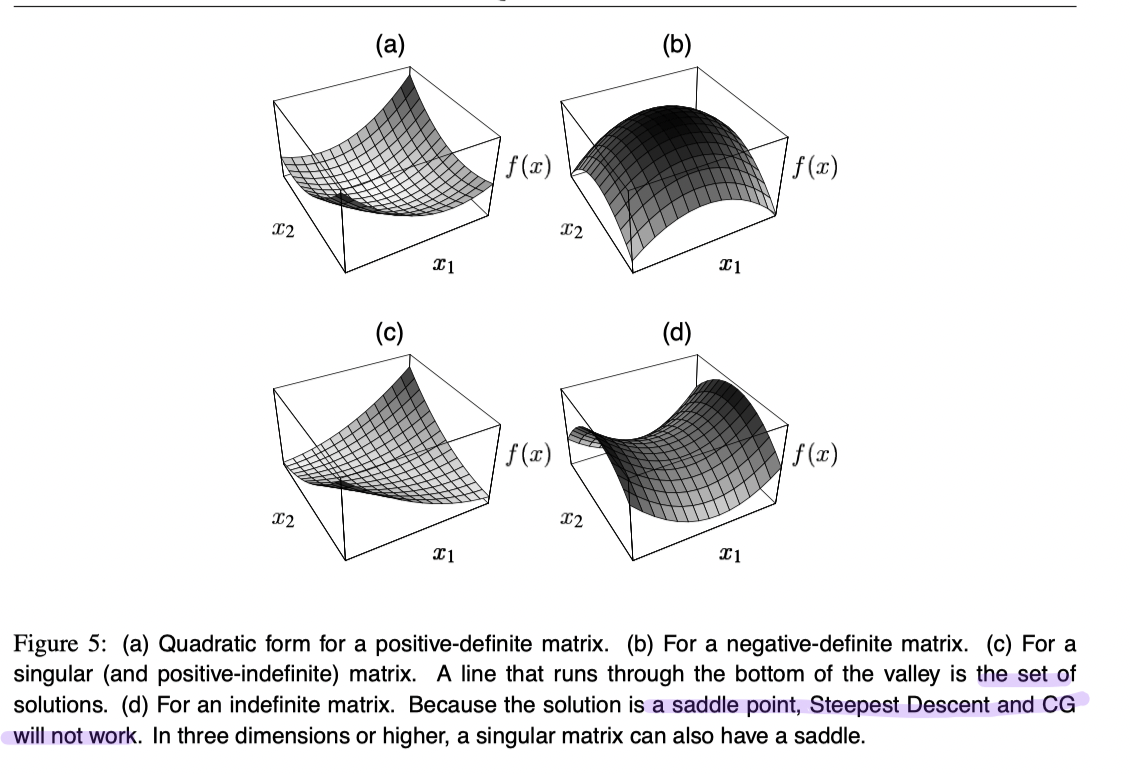
Different Situations w.r.t. positive or not
CG -- The Method of Steepest Descent
CG -- The Method of Conjugate Directions
The Method of Conjugate Gradients
High level idea
In CG -- The Method of Conjugate Directions we can set
Reason



Compute \beta
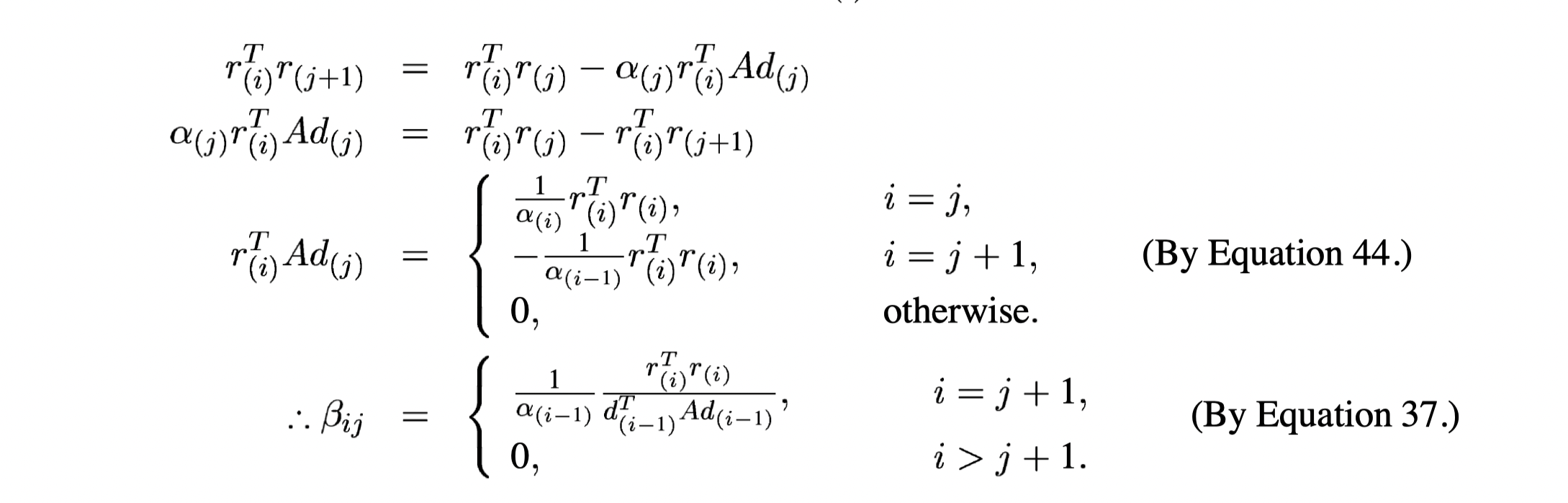
We don't need to memory all previous vectors like CG -- Gram-Schmidt Conjugation#Difficulties.
CG procedure
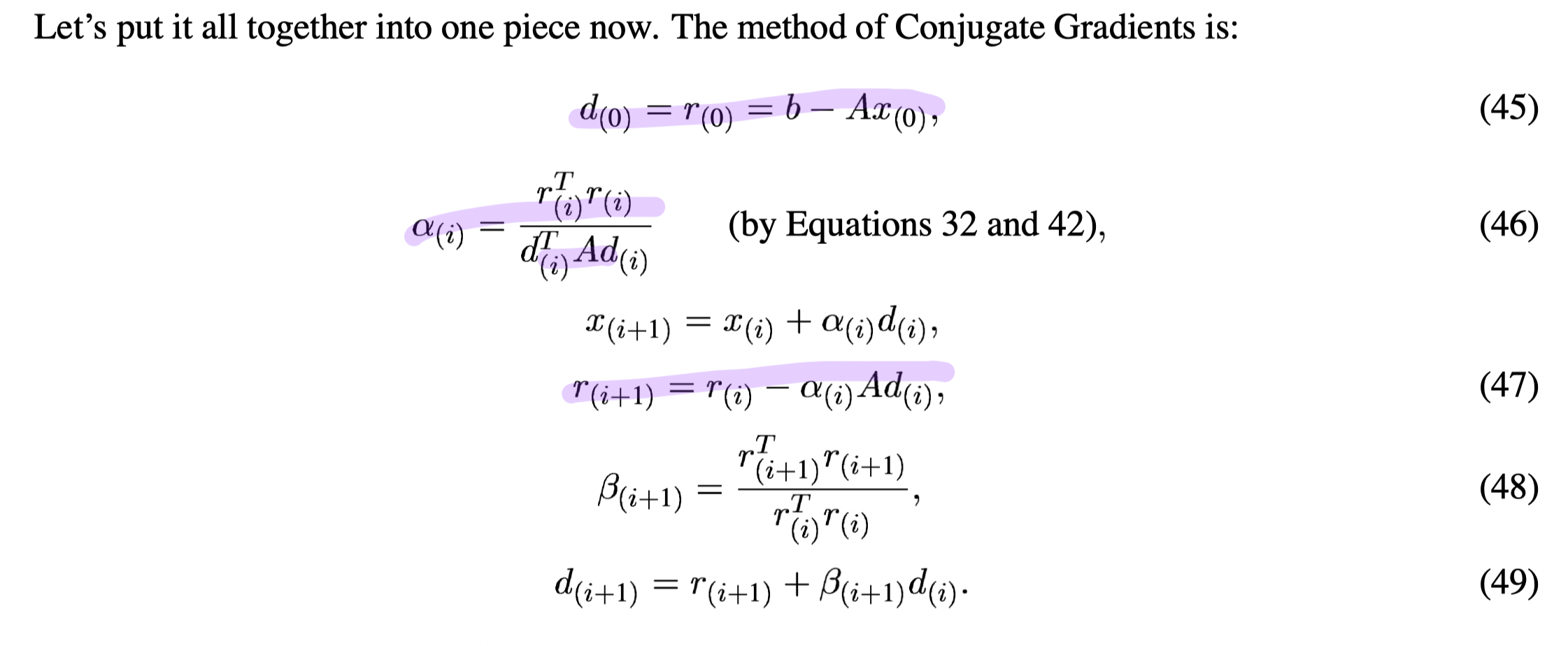
HPCG (Understand the preconditioned conjugate gradient method )