CG -- The Method of Conjugate Directions
High-level idea
CG -- The Method of Steepest Descent often finds itself taking steps in the same direction as earlier steps. So we have an idea to make it converge faster:
Let’s pick a set of orthogonal search directions
. In each search direction, we'll take exactly one step and that step will be just the right length to line up with . After steps, we'l be done.
Example
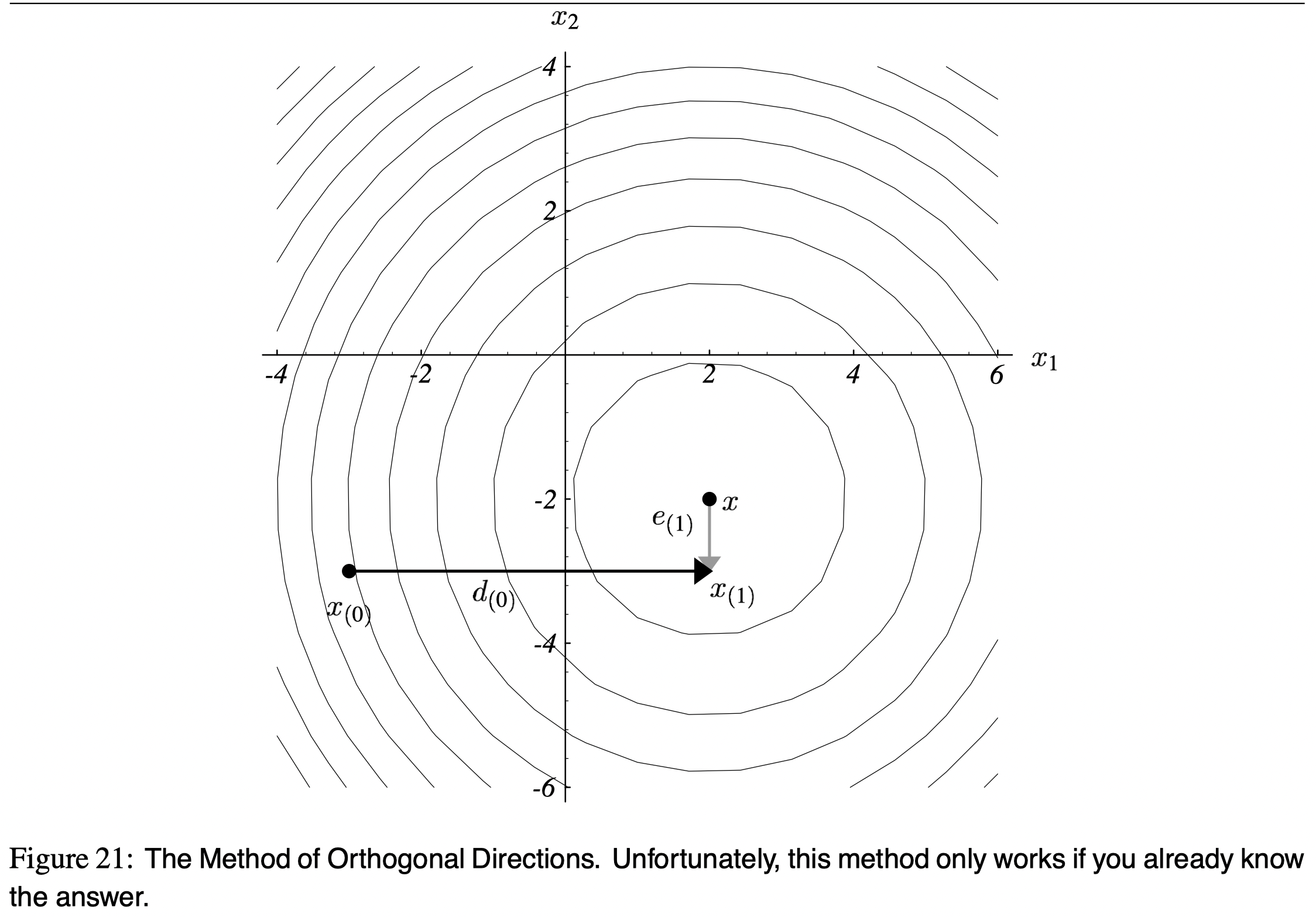
Update procedure
Compute \alpha
In order not to step in the previous directions (
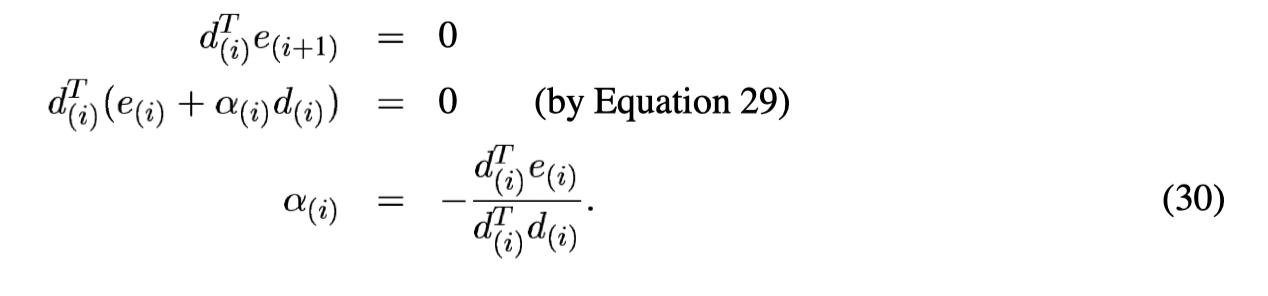
But we cannot do anything without knowing
A-orthogonal instead of orthogonal
Definition
Two vectors
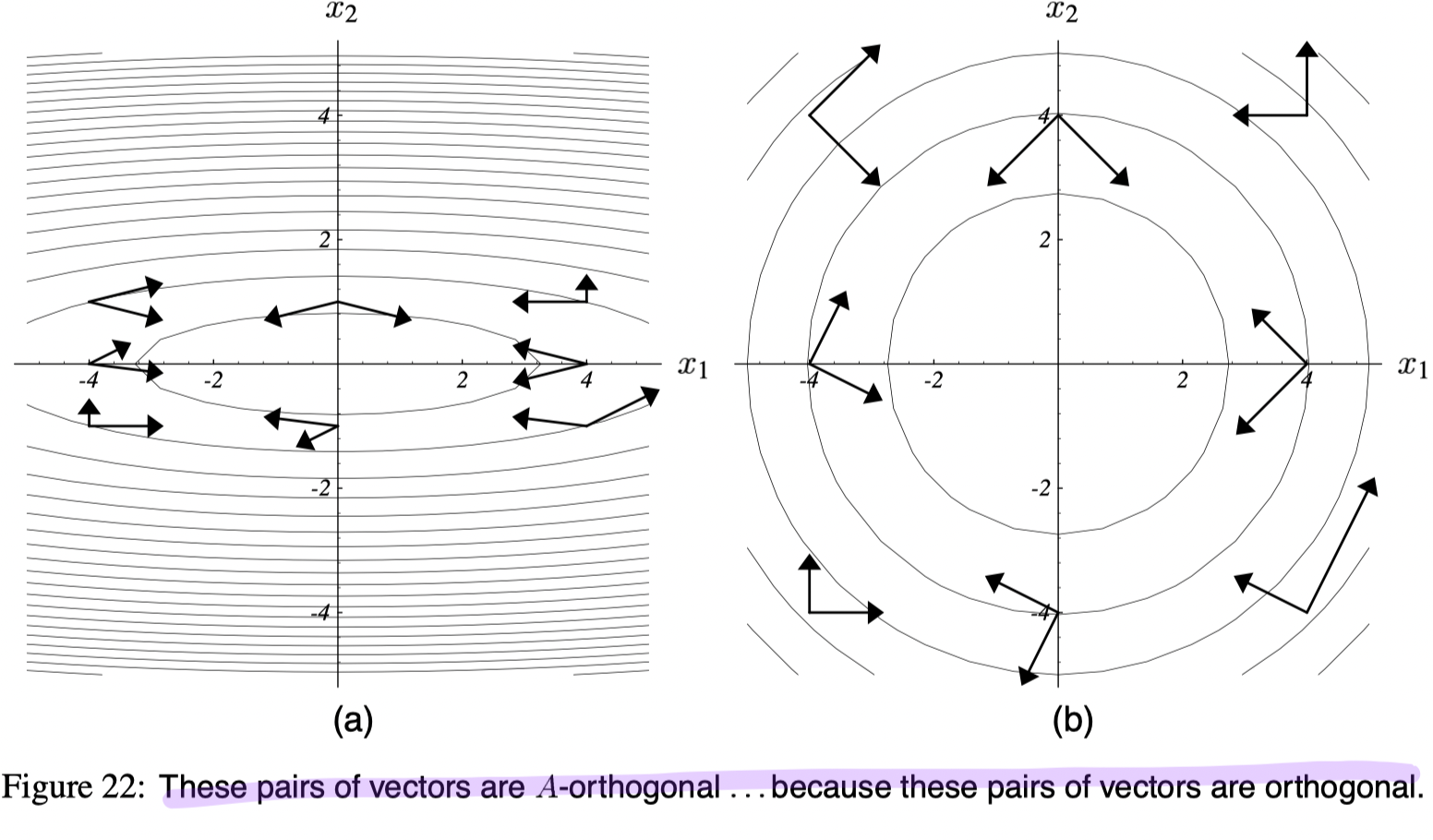
Thus,
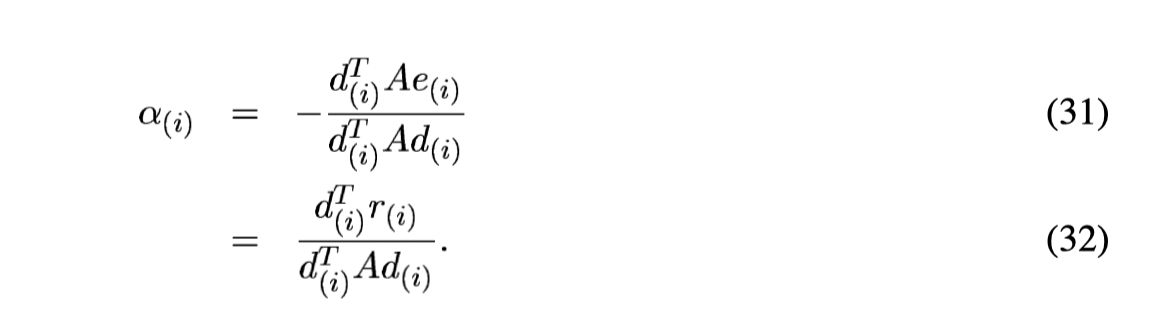
Prove we can compute

From the above formula, we concludes that
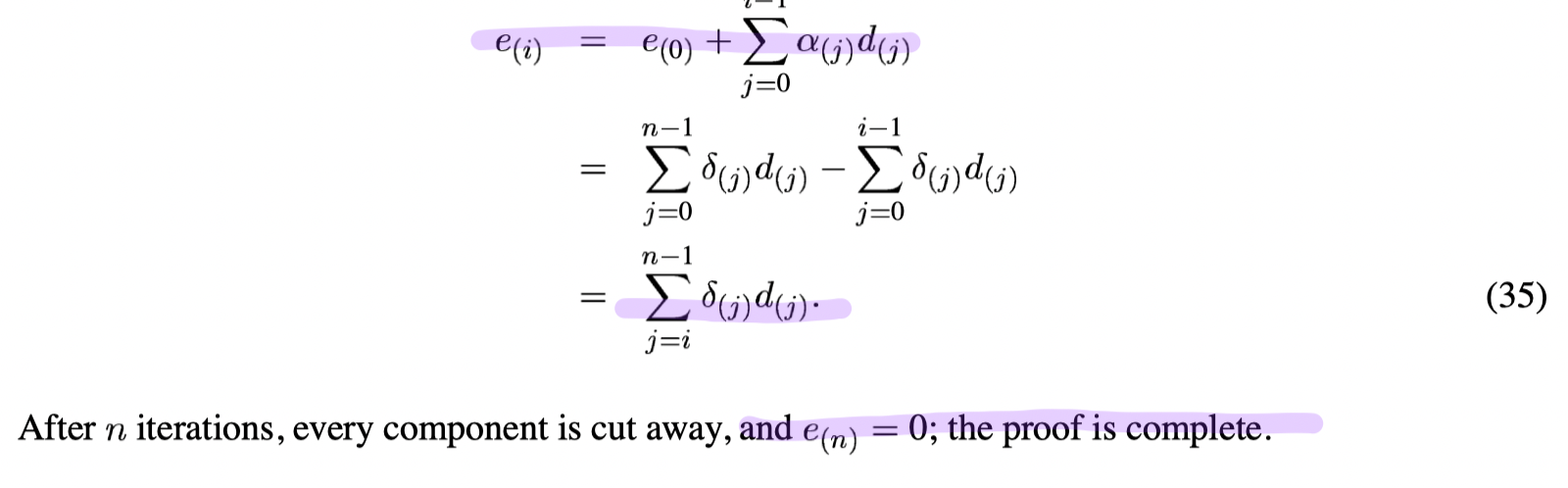
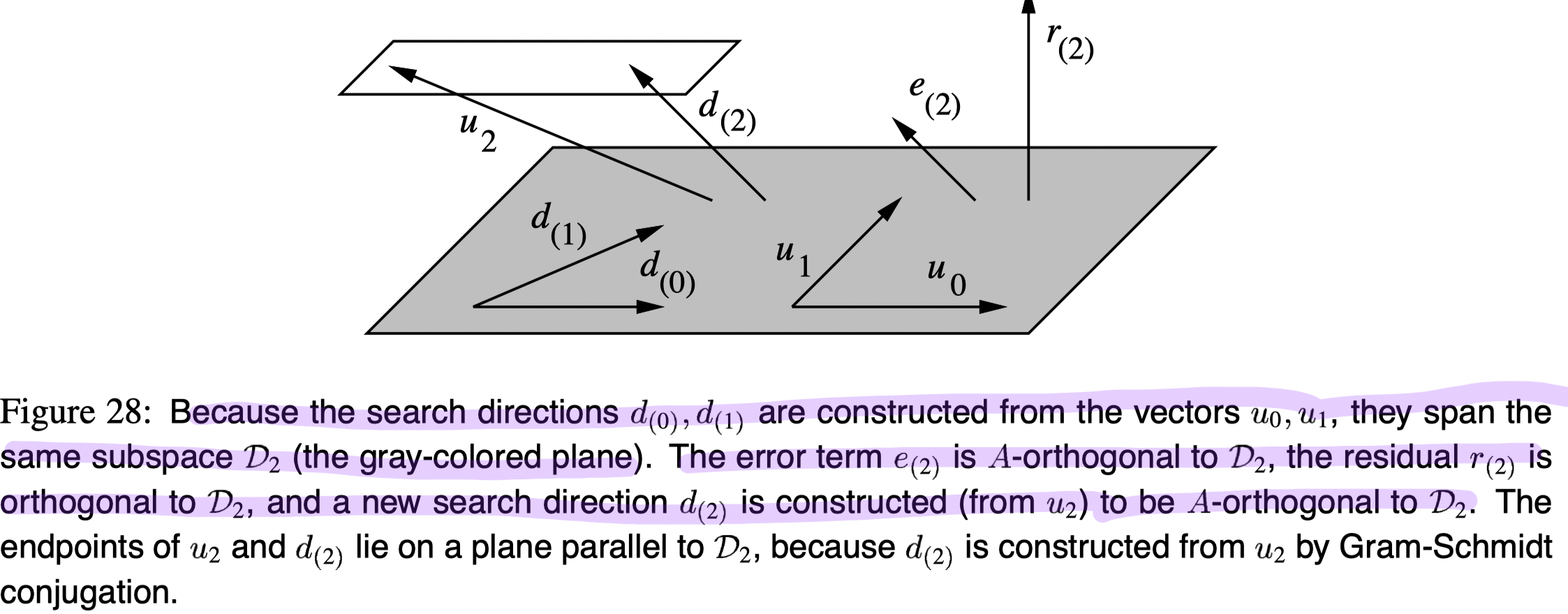
Construct
CG -- Gram-Schmidt Conjugation
Properties if using the Method of Conjugate Directions
- The error term is evermore A-orthogonal to all the old search directions since we never step back in the previous directions (Also from equation 35).
- From 1, since
, the residual is evermore orthogonal to all the old search directions, that is 
- From 2, because the search directions ({
}) are constructed from the vectors, the residual is orthogonal to these previous vectors, that is 
- From 2 and 3, we have
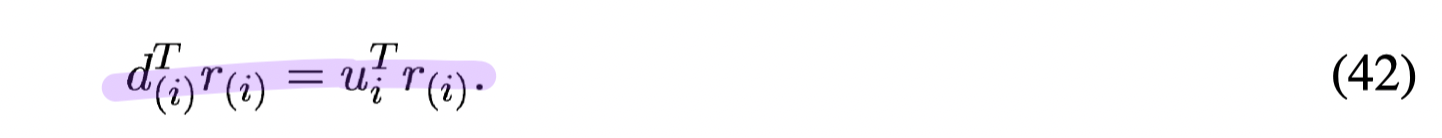
Info
New updates formula
